各教学院部:
现将2019—2020学年第2学期第10周创新创业学院有关工作通知如下:
一、关于上报近二十年大学生科技文化竞赛获奖情况的通知
根据《关于报送校史馆成就展布展材料的通知》要求,现对近二十年各教学院部获得的国际级、国家级金奖(特等奖、一等奖)情况进行上报,上报内容含获奖照片(原件或者扫描件)、比赛现场照片、获奖作品实物等。
(一)材料提交
1.大学生科技文化竞赛以承办学院为单位,按年度、赛事级别(国际级、国家级、省级)上报。
例:第一层级文件夹(**学院)→二层级文件夹(**年度)→三层级文件夹(国际级竞赛、国家级竞赛)→四层级文件夹(***竞赛)→竞赛照片
2.上报竞赛照片要标注名称。
例:****竞赛特等奖、***竞赛一等奖、***竞赛现场……
3.提交材料时,请同时提交材料清单。
(二)报送时间
各院部于5月8日前,将电子材料上报创新创业学院邮箱dzxycxcyxy2@163.com,将获奖实物送至创新创业学院办公室,请各请各教学院部负责竞赛的分管领导做好协调工作。
联系人:吴玉泾,联系电话:8983666
谢倩,联系电话:8987500
办公室:健行楼206房间;
二、关于2019年大学生科技文化竞赛创新活动成果汇编的通知
根据《德州学院大学生科技文化竞赛管理办法(2020年修订)》德院校办字〔2020〕4号文件要求,现进行2019年大学生科技文化竞赛活动成果汇编统计工作,所上报的获奖竞赛为德院校办字〔2020〕4号文件,附件2《德州学院大学生科技文化竞赛目录》中类别B及以上的竞赛,要求如下:
(一)竞赛名称;
(二)参赛简介:项目名称、项目成员(包括姓名、年级、专业、院系)、指导教师(姓名、研究方向)、项目介绍;
(三)项目上报的设计说明书等材料;请各教学单位通知相关负责教师于5月15日前将电子版发送至电子邮箱dzxycxcyxy2@163.com,上报文本格式参考《大学生科技文化竞赛获奖作品案例汇编格式》(见附件1),纸质版《大学生科技文化竞赛获奖作品案例汇编格式》,加盖公章,送至创新创业学院办公室。
联系人:吴玉泾,联系电话:8983666
谢倩,联系电话:8987500
办公室:健行楼206房间。
三、关于上报2020年《大学生科技文化竞赛活动方案》的通知
根据《德州学院大学生科技文化竞赛管理办法(2020年修订)》德院校办字〔2020〕4号文件及《德州学院大学生科技文化竞赛目录》,请各竞赛承办部门(学院)上报2020年各项大学生科技文化竞赛的活动方案。
(一)由承办单位编写《大学生科技文化竞赛活动方案》,竞赛活动方案内容要详细全面,内容包括:参赛周期、参赛范围、校赛方案、校赛一等奖设置规划及依据、校赛评审专家建议名单、项目培养方案、财务预算方案等内容。拟每项竞赛预算不超过2万元,拟每项竞赛设立校赛一等奖20个,各学院可根据承办的各项赛事特点制定具体方案。
(二)《大学生科技文化竞赛活动方案》于5月15日前将电子版发送至dzxycxcyxy2@163.com。纸质版《大学生科技文化竞赛活动方案》,加盖公章,上报创新创业学院办公室
联系人:吴玉泾,联系电话:8983666
谢倩,联系电话:8987500
办公室:健行楼206房间。
四、关于继续上报第六届中国“互联网+”大学生创新创业大赛校赛种子项目的通知
1.各学院要高度重视第六届中国“互联网+”大学生创新创业大赛校赛工作,广泛动员师生积极参与竞赛活动,深入挖掘校友资源,形成竞赛的群众性基础。
2.各学院在认真学习、参考历届互联网+大学生创新创业大赛优秀获奖项目基础上,发现、扶持、培养具有各学院专业特色的优势项目,在第一次上报项目的基础上继续挖潜优秀项目。
3.各学院要充分发挥创新创业社团的作用,认真组织,积极实施,广泛动员学生积极参与,争取参赛单位取得 优异成绩。
4.全国大学生创业服务网:https://cy.ncss.cn/
5.校赛工作邮箱:dzxycxcyxy2@163.com
联系人:吴玉泾,联系电话:8983666
谢倩,联系电话:8987500
办公室:健行楼206房间。
附件:1.大学生科技文化竞赛获奖作品案例汇编格式
创新创业学院
2020年4月30日
附件1
大学生科技文化竞赛获奖作品案例汇编格式
目 录
一、中国“互联网+”大学生创新创业大赛
赛事简介…………………………………………………………1
1.项目名称(XX年XX等奖作品)
xx级XX学院XXX等指导教师XXXX………………………2
二、“挑战杯”全国大学生课外学术科技作品和创业计划竞赛
赛事简介………………………………………………………
1.项目名称(XX年XX等奖作品)
xxx级XX学院XXX等指导教师XXXX………………………
……
项 目 名 称
赛事简介
成员:张训汉2005级信息与计算科学计算机系
刘亚丽2005级数学与应用数学数学系
杨莉莎2005级信息与计算科学数学系
指导教师:高秀莲
获奖级别:全国大学生数学建模竞赛国家级A二等奖
项目介绍:
第29届奥运会在北京举行,大量观众到现场观看奥运比赛,其中大部分人将会乘坐公共交通工具(简称公交,包括公汽、地铁等)出行。这些年来,城市的公交系统有了很大发展,北京市的公交线路已达800条以上,使得公众的出行更加通畅、便利,但同时也面临多条线路的选择问题。针对市场需求,某公司准备研制开发一个解决公交线路选择问题的自主查询计算机系统。
为了设计这样一个系统,其核心是线路选择的模型与算法,应该从实际情况出发考虑,满足查询者的各种不同需求。请你们解决如下问题:
1、仅考虑公汽线路,给出任意两公汽站点之间线路选择问题的一般数学模型与算法。并根据附录数据,利用你们的模型与算法,求出以下6对起始站→终到站之间的最佳路线(要有清晰的评价说明)。
(1)、S3359→S1828 (2)、S1557→S0481 (3)、S0971→S0485
(4)、S0008→S0073 (5)、S0148→S0485 (6)、S0087→S3676
2、同时考虑公汽与地铁线路,解决以上问题。
3、假设又知道所有站点之间的步行时间,请你给出任意两站点之间线路选择问题的数学模型。
乘公交,看奥运
——公交路线查询系统
摘要:本文将附件提供的公交线路信息视为相应的北京市公交网络图,在此基础上,通过合理的假设,我们针对任意两公交站点路线选择问题建立了求两个任意站点间最短有向路径的0-1规划模型。
针对问题一在知道城市公交特点(公交网络在设置时已充分考虑了换乘次数即任意不可直达的两站间的最优路径上换乘次数不会超过两次)的前提下,以换车次数最少为首要目标,在换车次数相等的情况下,将时间最短列为第二目标,若出现耗时相等的路线,则再考虑票价的影响。从而将问题转化为网络优化问题并建立了0-1规划模型。为了验证模型的可行性,我们将问题一中的6个起始站
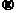 终点站的最优路线利用问题一的思想并用Matlab7.0编程求解,结果如下:
终点站的最优路线利用问题一的思想并用Matlab7.0编程求解,结果如下:
起点站 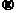 终点站 终点站
|
经过的站点数(包括起始站和终点站) |
最短时间(分钟) |
最少费用(元) |
S3359→S1828 |
33 |
101 |
2 |
S1557→S0481 |
35 |
109 |
3 |
S0971→S0485 |
43 |
128 |
3 |
S0008→S0073 |
27 |
81 |
2 |
S0148→S0485 |
33 |
106 |
3 |
S0087→S3676 |
21 |
65 |
2 |
针对问题二中提供的两条地铁线路的信息,沿用问题一的建模思想,全面的考虑了不同类型站点的换乘方式(公汽与公汽换乘,公汽与地铁,地铁与公汽和地铁与地铁间的换乘),对目标函数中的价值向量进行了恰当的修改。在求解过程中我们利用了一种比较方便的改进了的算法,即将出现在同一地铁站点附近的公汽站点均用该地铁站点表示,利用模型一的解法进行求解,从而大大减小了工作量。问题二的结果如下:
起点站 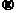 终点站 终点站
|
经过的站点数(地铁站和公汽站) |
最短时间(分钟) |
最少费用(元) |
S3359→S1828 |
33 |
101 |
2 |
S1557→S0481 |
35 |
109 |
3 |
S0971→S0485 |
34 |
96 |
5 |
S0008→S0073 |
27 |
81 |
2 |
S0148→S0485 |
31 |
88 |
5 |
S0087→S3676 |
11 |
25 |
3 |
作为问题一二的延伸,问题三中假设任意两站间的步行时间已知,将原来的有向图转化成了完全有向图,从而加大了运算量,但相应的也提高了模型的实际意义。针对问题三我们也建立了0-1规划模型,其中价值向量取相邻两站点间所耗的最小值。即原有向图中的
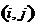 弧的权为3,原有向图中不存在的
弧的权为3,原有向图中不存在的
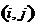 弧的权为步行时间,从而将问题转化为求有向网络中的最短有向路问题。对于该模型,考虑到算法的复杂性以及题目中并未给出步行时间的具体数据,我们只给出了求解思路未对其求解。
弧的权为步行时间,从而将问题转化为求有向网络中的最短有向路问题。对于该模型,考虑到算法的复杂性以及题目中并未给出步行时间的具体数据,我们只给出了求解思路未对其求解。
一 问题重述与提出
随着科技的发展环境保护已成为当今世界的主要话题。我国人民翘首企盼的第29届奥运会明年8月将在北京举行,届时有大量观众到现场观看奥运比赛,为了符合奥运会的理念中“绿色奥运”,并缓解奥运会带来的道路压力,以公共交通工具替代私家车,出租车已经成为一种趋势,将会有大部分人乘坐公共交通工具(简称公交,包括公汽、地铁等)出行。
近年来,城市的公交系统有了很大发展,北京市的公交线路已达800条以上,使得公众的出行更加通畅、便利,但同时也面临多条线路的选择问题。在奥运会即将来临之季,某公司针对市场需求准备研制开发一个解决公交线路选择问题的自主查询计算机系统。
自主查询计算机系统核心是线路选择的模型与算法,应该从实际情况出发考虑,满足查询者的各种不同需求。需要解决如下问题:
1、仅考虑公汽线路,给出任意两公汽站点之间线路选择问题的一般数学模型与算法。并根据附录数据,利用你们的模型与算法,求出以下6对起始站→终到站之间的最佳路线(要有清晰的评价说明)。
(1)、S3359→S1828 (2)、S1557→S0481 (3)、S0971→S0485
(4)、S0008→S0073 (5)、S0148→S0485 (6)、S0087→S3676
2、同时考虑公汽与地铁线路,解决以上问题。
3、假设又知道所有站点之间的步行时间,请你给出任意两站点之间线路选择问题的数学模型。
…… ………… ……… …… ……
